Dove vai pensiero?
- Ottero. I testi biblici riportano numerose situazioni in cui gli uomini eletti ebbero un contatto con l’Entità che spiega l’infinito, ma anche per essi il Mistero rimaneva tale. La voce e la manifestazione di volontà dell’Entità era palese per loro, ma forse neppure così riuscirono a darsene una spiegazione, a vederne lo scopo ultimo, a leggere nella Mente che governa il Cosmo intero. Noè arrivò, così è tramandato, alla rispettabile età di seicento anni per accettare di farsi strumento dell’Entità e dei suoi piani. Durò un anno la sua avventura che consentì di realizzare un’intenzione superiore di purificazione del rapporto fra l’uomo e il suo Creatore. Il “Genesi” descrive con dovizia di dettagli quegli eventi straordinari, ma colloca, con tutto ciò, l’uomo nella limitata condizione di esecutore, un uomo che pone in essere con meticolosa cura ogni indicazione ricevuta, che è partecipe solo passivamente di una volontà suprema nel momento della sua realizzazione. Un uomo, assurto a simbolo dell’umanità colpevole ed espiante, immerso in una realtà imprevedibile permeata dal caos e asservita al caso, un uomo che in certi istanti viene a contatto con le proprie illusioni, e crede.
- Mirach. Oggi noi abbiamo imparato qualcosa dalla storia, dalle illusioni, dagli eventi biblici, dalla nostra stessa insoddisfazione. Abbiamo capito che non esiste un “Apriti, Sesamo!”. Le porte che aprono al vuoto inconcepibile le dobbiamo spalancare noi stessi, con le nostre forze. Volgo lontano i miei occhi e imploro a gran voce: “Quando mi togli da questa palude?!”.
- Tosco. Ma, dài! Che vai a dire! Io, in questa palude, ci sguazzo bene anzichenò. Se ne esci, come potrai continuare a tormentarti le meningi, così come ci è congeniale, a tutti noi, quando ci troviamo insieme? Io propongo di scendere lesti lesti da quelle entità tanto irraggiungibili quanto meno osservabili. Propongo, dunque, di scendere a patti con la concretezza che ben conosciamo, quella della realtà quotidiana.
- Mirach. Che significa, questo? Significa che speculare per astrazione dovrà esser bandito dai nostri confronti concettuali? Vuoi dunque ridurre la sostanza delle nostre dissertazioni al mondo della materia?
- Tosco. Capisco, e ti tranquillizzo. Vedrai che non ho alcuna intenzione di uscire dal seminato. E, per dimostrartelo, inizio subito con un rompicapo, muovendomi nel contesto delle conoscenze geometriche, dalla cosa più piccola che c’è, mi sai dire quale?
- Mirach. Ma… vuoi dire l’atomo, anzi, l’elettrone o il neutrino o il quark…
- Tosco. No, no, nulla del genere, quella è fisica delle particelle, è roba subnucleare, non geometria. Io invece parto dall’entità geometrica più piccola che si possa immaginare: il punto.
- Mirach. Il punto?
- Tosco. Sì, ora lasciami dire. Mi è venuta un’idea originale, quella del primo punto. Ma, prima di procedere, fermiamo l’attenzione sul significato della parola “punto”. Se tu apri un qualsiasi dizionario e vi cerchi la definizione di “punto” leggerai che si tratta di un concetto primitivo della geometria, che può essere rappresentato soltanto in modo intuitivo come una figura geometrica priva di qualsiasi dimensione: dunque un punto non è largo né lungo né alto né spesso né profondo, eccetera eccetera. Ecco che, allora, il significato che si accompagna alla parola “punto” riporta a qualcosa di intangibile, che non esiste nella realtà; sebbene la definizione del vocabolario faccia uso del termine “figura” geometrica – e la figura non è tale se non ha un riscontro sensibile da parte di un apparato percettore – il punto si riduce necessariamente a una creazione concettuale, a un’ipotesi. Non avendo dimensioni fisiche né geometriche, il punto non può neppure essere rappresentato graficamente. Esiste come astrazione nel mio mondo rappresentativo interno e, come tale, resta incomunicabile. Posso disegnare un triangolo, un pentagono in quanto traccio un perimetro delimitante una superficie piana e posso comunicarne ad altri la definizione nel momento in cui ne indico la forma: “questo è un triangolo”. Ma non posso fare lo stesso con un punto. Non lo posso indicare nello spazio né il mio interlocutore lo può percepire visivamente, dal momento che non ci sono dimensioni da cogliere. Ne posso condividere l’essenza, non già l’esistenza, mediante la rappresentazione mentale di una rappresentazione mentale che viene condivisa per un atto intuitivo, su scala puramente astratta dunque.
- Ottero. Perbacco, è un’idea formidabile. Il cosiddetto punto mi porta d’un tratto a pensare a un modo comunicativo tutto particolare. Già, perché se uso il linguaggio, la grafica, il comportamento motorio per comunicare a un mio interlocutore il concetto di triangolo, come avviene nell’insegnamento accademico in verità, io riesco a trasmettere un’idea che esiste nella mia mente, a un’altra mente la quale, con il supporto degli afferenti sensoriali e dei sistemi di codificazione semantica, fissa in schemi di elaborazione e di memoria il concetto acquisito. Tutto l’insegnamento si realizza in questo processo di scambio figurativo concettuale. Non è certo possibile apprendere un concetto nuovo, a livello di pura astrazione, se non si possiedono anteriormente le basi cognitive adeguate perché quel concetto trovi un aggancio al quale ancorarsi. La cultura umana, in fin dei conti, che cos’è se non un apprendimento amplificato per continua trasmissione di informazioni da modalità concrete-esperibili a modalità sempre più astratte-rappresentabili? È una progressione inarrestabile: si evolverà fin tanto che riusciremo a comunicare fra mente e menti essenzialmente sul piano delle pure astrazioni, come accade quando ci soffermiamo attorno all’idea di punto. Questo, infatti, da punto geometrico che non esiste, che non può esistere per mancanza di requisiti, diventa punto rappresentazionale. Finiremo, come forse già sta accadendo per civiltà estremamente progredite con le quali non siamo ancora in contatto o, se più ci piace, ancora non sappiamo di essere in prolungato contatto, finiremo, dicevo, per fare a meno della iconografia, della misurazione, della descrizione, persino del linguaggio. La nostra sarà essenzialmente una comunicazione di e per rappresentazioni mentali senza supporti sensibili, veicolate per astrazioni e intuizioni immediate. Oppure, paradosso per paradosso, così già eravamo tanto e tanto tempo fa, prima che sopraggiungesse il linguaggio, questa forma cristallizzata di comunicazione che tutto sistema in categorie, tutto classifica, tutto ordina secondo canoni logici e circoscritti. Ora che le nostre competenze linguistiche sono pervenute a un limite di esasperazione per complessità, poliedricità e versatilità di utilizzo, a seconda degli scopi che si vuole ottenere, ora che l’estrema sofisticatezza del codice linguistico sta trasformando la chiarezza del comunicato in confusione per la possibilità ampiamente a portata di mano di giocare con percetti, concetti e significati conformemente alle contingenze e al contesto comunicativo, proprio ora pare che il linguaggio stesso dia i primi segni di sfaldamento. Un codice comunicativo come quello linguistico ha finito per esaurire la propria energia creativa e ha preso a sostituire comprensione con caos ideativo, deludendo le nostre aspettative di conoscenza, di chiarezza e facendo largo all’onda anomala delle parole per se stesse, spoglie di un significato corroborante.
- Tosco. Grazie per la tua dotta digressione, la reputo molto interessante. E, proprio per questo, vorrei dire ancora qualcosa su quell’idea del primo punto che, secondo me, contiene una straordinaria forza di originalità. Dunque, torniamo al nocciolo del discorso. Se il “punto” non può essere rappresentato graficamente, tanto meno lo si può misurare o collocare in una qualche parte specifica dello spazio. Un’altra definizione che gli si potrebbe attribuire sarebbe allora quella di estrema riduzione/atomizzazione di un qualsiasi luogo geometrico sensibile. Ma mi rendo conto che questa non è una definizione poiché, portata all’eccesso, conduce allo zero assoluto; è una negazione piuttosto che una definizione.
- Tiziano. Una “negazione”! Accidenti, di tanto in tanto le tue parole hanno il potere di risvegliare nella mia mente associazioni curiose. Posso interromperti un attimo?
- Tosco. Prego, accomodati… l’hai già fatto!
- Tiziano. Mmm, sì, scusa… Allora, negazione, estrema riduzione, involuzione, assorbimento, regressione, inversione di ciclo. Avete tutti capito a che cosa sto pensando, vero? Ma sì, “The Black Holes”, i buchi neri, lo stomaco insaziabile delle galassie, l’estrema riduzione, l’estremo eterno ritorno di tutte le cose in una dimensione involuta e involutiva, il mistero dei misteri delle dinamiche cosmiche. Il punto postulato dalla geometria nella sua stessa evoluzione come scienza costituisce un campo di argomentazione che merita una considerazione di tutto privilegio. A iniziare dalla geometria euclidea attraverso lo sviluppo di sistemi assiomatico-deduttivi, sino all’affermarsi della geometria analitica e al suo proliferare sotto le spoglie di geometria algebrica e di geometria differenziale, s’è visto che un postulato come quello di “punto” non può e non deve fermarsi a una definizione, proprio per il fatto che tale postulato risulta immerso in una soluzione speculativa alquanto arbitraria e del tutto convenzionale. A partire da queste posizioni non sono forse autorizzato a liberare il mio pensiero verso la ricerca di una qualche affinità tra un buco nero galattico e un punto nella mia rappresentazione mentale? Nella sostanza c’è qualche differenza? Le differenze le creiamo noi, riducendo ogni cosa a scale dimensionali, a tipologie dinamiche o funzionali e, meno ci riusciamo a capire, più vi cuciamo attorno una pletora di fronzoli che ci dilettiamo a chiamare con l’appellativo di “scoperte scientifiche”.
- Tosco. Formidabile! La tua creatività immaginativa ci porterà un giorno o l’altro molto lontano. Ora, dopo che ti ho seguito un po’ a fatica, devo ammetterlo, farei un balzo da quel buco nero e tornerei rapidamente al mio concetto di punto. Non temere, peraltro, di interrompermi, quando ti punge lo stimolo. Bene, prendiamo una figura qualsiasi della geometria piana. Posso dire “il triangolo è una figura piana chiusa e delimitata da tre linee rette che si intersecano vicendevolmente sullo stesso piano”. Ma poi devo ricorrere a un feed-back e curare di definire che cos’è un piano, che cos’è una linea retta, che cosa intendo per “figura”. Mi è difficile trovare le giuste formulazioni. Potrei riuscirci meglio con una rappresentazione grafica. Restando al nostro “punto” mi risultano impossibili entrambe le cose, sia la definizione sia la rappresentazione grafica. A meno che dia piena licenza all’immaginazione e prenda la determinazione di rappresentare il punto con un segno su un foglio di carta. Resti ben inteso, sto costruendo un ibrido di astrazione e concretizzazione, ma questo soltanto a fini comunicativi, altrimenti non troverei altra via per spiegarmi.
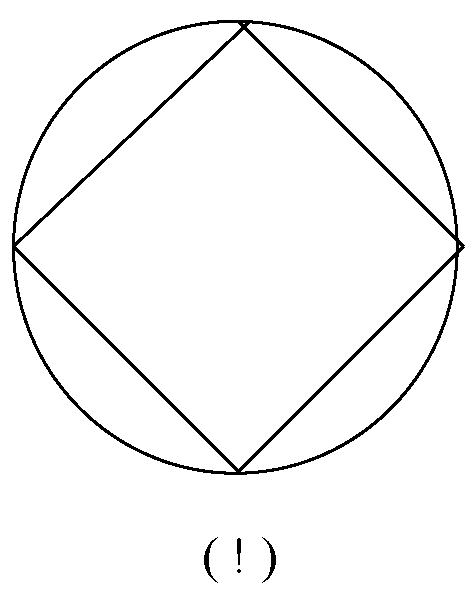
- Dunque segno un punto sulla carta, come per dire “metto un punto qui”. Poi segno altri tre punti equidistanti fra di loro e rispetto al primo, diametralmente opposti su una immaginaria circonferenza. Non ancora considerando quest’ultima, se congiungo i quattro punti ottengo un quadrato con i lati inclinati di 45° sulla linea orizzontale di appoggio. Ora passiamo alla progressiva smembratura dei quattro lati del quadrato sino a trasformare questo in un cerchio. Come? Coprendo la distanza fra i punti originari, quelli che congiungono i quattro lati del quadrato, mediante l’inserimento di altri punti equidistanti sia dal centro del campo – ossia dal punto di intersezione delle due diagonali del quadrato, che sono anche diametri del futuro cerchio, normali fra di loro – sia dai precedenti punti che vengono a trovarsi a lato. Ora ripeto l’operazione, più e più volte. È chiaro che sto parlando in termini di progressione geometrica: i punti iniziali, in numero di 4, diventano a mano a mano 8, 16, 32, 64 e così via. Quanti punti troveranno posto su questa circonferenza in fieri? Quante volte dovrò ripetere l’operazione di dimezzamento delle distanze e quanti punti dovrò aggiungere, nella mia progressione geometrica, per ottenere un cerchio chiuso? O forse è più confacente domandarsi “quanti punti devo segnare perché la mia capacità percettiva pervenga a riconoscere la «gestalt»[1] di un cerchio?”. È evidente che, a muovere dai quattro punti iniziali, per mezzo dei quali sono portato a riconoscere grosso modo la struttura di un quadrato, per portare la configurazione a 8 punti con l’intuizione della figura di un ottagono regolare, di lì in avanti, più raddoppiamenti eseguo nella densità dei punti più mi allontano dall’intuire la forma di un poligono e più mi avvicino a quella di cerchio. Il momento preciso di passaggio del riconoscimento intuitivo dalla forma di poligono a quella di cerchio non riuscirò a coglierlo. È, ancora, uno di quei momenti/non-momenti di per sé inafferrabili, similmente al passaggio dalla veglia al sonno, dal dì alla notte, dal caldo al freddo e così via. Ma quando finirò di raddoppiare i punti, quando avrà termine questa progressione geometrica fatta di entità geometriche invisibili, indescrivibili e tuttavia oggetto di percezione sensibile e di rappresentazione concettuale? Risposta: mai, per il semplice motivo che quei punti non hanno dimensioni e non occupano spazio.
[1] Gestalt: Corrente psicologica centrata sulla percezione di una figura nella sua forma strutturale, non tanto come sintesi di elementi sensoriali.
Immagine di Copertina tratta da Free Daily Bible Study.

